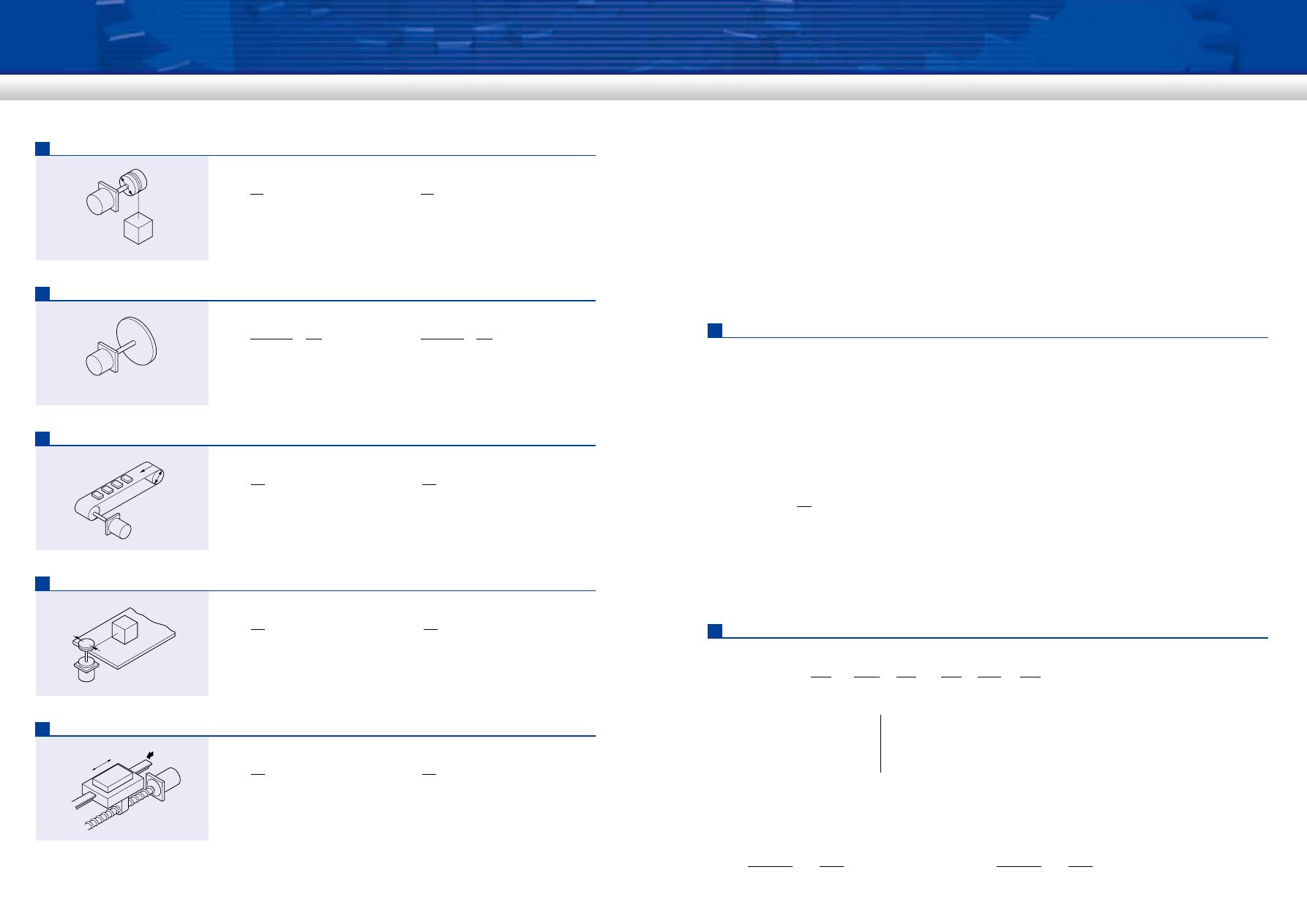
許容慣性負荷の確認

ギヤヘッドの連結されている負荷慣性モーメント（J）が大きい場合、頻繁な断続運動の起動時（または電磁ブレーキおよ
びブレーキユニットによる停止時）に、瞬間的に大きなトルクが発生します。この衝撃負荷が過大であると、ギヤヘッド
およびモータの破損につながる場合があります。また、負荷の種類によって慣性は異なりますので、参考として各種形
状による慣性の求め方を別表（A-52∼A-53ページ）に示しました。ブレーキを使用する場合、負荷の慣性が歯車や電
磁ブレーキの寿命に大きく影響します。したがって、電磁ブレーキやブレーキユニットを使用して制動する場合は、各
機種ごとに設定している負荷の許容慣性を超えない範囲でご使用ください。三相モータの許容負荷慣性は、一旦停止して
から逆転させる場合の値です。

・ モータ軸における負荷慣性は次式で求めてください  
  （SI単位系）

J

M

 

＝ J

G

  ×

 J

G

  ：ギヤヘッド出力軸慣性モーメント〔kg・cm

2

〕

 J

M

  ：モータ軸許容慣性モーメント〔kg・cm

2

〕

   i  ：減速比（例：1/5ならば i ＝5）
※GD

2

で算出する場合も、同様の計算式となります。

モータと負荷慣性

モータで慣性負荷を回転させるときの運動方程式は、次のようになります。

ここにT：トルク〔N・m〕
J   ：慣性モーメント 〔kg・m

2

〕

ω  ：角速度 〔rad/s〕

t  ：時間 〔s〕
n  ：回転速度 〔r/s〕

誘導電動機の場合、モータの立上り時のトルクは、回転速度によって変化します。そこで、始動から定速までの平均を
とり平均加速トルクと呼んで一般に使用しています。J〔kg・cm

2

〕

（GD

2

〔kgf・cm

2

〕）なる慣性負荷を時間  t〔s〕の間に

回転速度 n〔r/min〕まで加速する時に必要な平均加速トルク T

A 

は次式で求められます。

・SI単位系 

 

 

        ・重力単位系

i

2

1

T ＝ Jα ＝ J・   ＝  ・  ＝  ・  ・

T

A

＝      ×     

〔N・m〕

dω

dt

dω

dt

dn

dt

2π

60

GD

2

4

GD

2

4

J

9.55 × 10

4

N

t

T

A

＝      ×     

〔kgf・cm〕

GD

2

3750000

N

t

減速比1/3∼1/50の場合 

J

G

  ＝  J

M

  ×  i

2

減速比1/60以上の場合  

J

G

  ＝  J

M

  × 2500

J

G

 ：ギヤヘッド出力軸許容慣性〔kg・cm

2

〕

J

M

 ：モータ軸許容慣性〔kg・cm

2

〕

 i  ：減速比〔例：1/5ならば i ＝ 5 〕
モータ軸の許容慣性〔＝J

M

〕は、モータによって異なり

ますので、別表（A-50∼A-51ページ）を参照願います。

モータを取扱う時の慣性モーメントの表し方として J や GD

2

 が用いられますが、J は一般的にイナーシャと呼ばれSI単

位系での物理的な慣性モーメントと同値となります。単位は〔kg・m

2

〕を用います。

一方GD

2

（ジーディースクエア）はフライホイール効果等とも呼ばれ、従来の単位系である重力単位系での工業的な計

算によく用いられます。単位は〔kgf・m

2

〕または〔kgf・cm

2

〕を用います。JとGD

2 

の数値としての関係は

J＝GD

2

／4

となっています。
本カタログで慣性を表す場合、SI単位系では  J、重力単位系では  GD

2

  として併記しています。またJの単位は力学的な意

義より、本来は〔kg・m

2

〕を使うべきですが、計算を簡単にするため〔kg・cm

2

〕を本カタログでは使用しています。各

種負荷の形状からの J やGD

2

 の求め方は別表（A-52∼A-53ページ）を参照してください。

・ギヤヘッド出力軸における許容負荷慣性モーメントは
 次式で求めてください。

GD

2

 ：フライホイール効果 〔GD

2

＝4J〕

g  ：重力の加速度g＝9.8 〔m/s

2

〕

α  ：角加速度 〔rad/s

2

〕

荷重を巻き上げる場合

□ SI 単位系

□ 重力単位系

モータ

D

W

ベルト車

モータ

W

D

F

W

D

モータ

モータ

はずみ車

ベルト車

F

W

μ

P

Ｔ＝  Ｄ・Ｗ〔N・m〕

Ｄ：ドラム直径 〔m〕
Ｗ：荷 重 〔N〕

1
2

Ｔ＝  Ｄ・Ｗ〔kgf・m〕

Ｄ：ドラム直径 〔m〕
Ｗ：荷 重 〔kgf〕

1
2

□ SI 単位系

□ 重力単位系

Ｔ＝     ・  〔N・m〕

Ｎ：回転速度 〔r/min〕
Ｊ：イナーシャ〔kg・cm

２

〕

ｔ：時 間 〔s〕

Ｊ

9.55×10

4

Ｎ
ｔ

Ｔ＝     ・  〔kgf・m〕

Ｎ   ：回転速度 〔r/min〕

ＧＤ

2

：フライホイール効果〔kgf・cm

２

〕

ｔ    ：時 間 〔s〕

ＧＤ

2

3750000

Ｎ
ｔ

□ SI 単位系

□ 重力単位系

Ｔ＝  Ｄ（Ｆ＋μＷｇ ）〔N・m〕

Ｄ：ローラの直径 〔m〕
Ｗ：負荷の質量〔kg〕
ｇ：重力加速度〔ｍ/s

２

〕

μ：摩擦係数
Ｆ：外 力〔N〕

1
2

Ｔ＝  Ｄ（Ｆ＋μＷ ）〔kgf・m〕

Ｄ：ローラの直径 〔m〕
Ｗ：負荷の重量〔kgf〕
μ：摩擦係数
Ｆ：外 力〔kgf〕

1
2

□ SI 単位系

□ 重力単位系

Ｔ＝   Ｐ（Ｆ＋μＷg）〔N・m〕

Ｆ：外 力〔N〕
Ｗ：負荷の質量〔kg〕
μ：摺動面摩擦係数〔 0.05∼0.2程度〕
ｇ：重力加速度〔ｍ/s

２

〕

Ｐ：ボールネジリード〔m〕

1

2π

Ｔ＝   Ｐ（Ｆ＋μW）〔kgf・m〕

Ｆ：外 力〔kgf〕
Ｗ：負荷の重量〔kgf〕
μ：摺動面摩擦係数〔 0.05∼0.2程度〕
Ｐ：ボールネジリード〔m〕

1

2π

□ SI 単位系

□ 重力単位系

Ｔ＝  Ｄ・μＷｇ〔N・m〕

Ｄ：ドラム直径〔m〕
Ｗ：質量〔kg〕
μ：摩擦係数

1
2

Ｔ＝  Ｄ・μＷ〔kgf・m〕

Ｄ：ドラム直径〔m〕
Ｗ：重量〔kgf〕
μ：摩擦係数

1
2

ベルトコンベアの場合

接触面を水平移動する場合

ボールネジを駆動する場合

慣性体を駆動する場合

A-49

慣性について

A-48

モータの選定

負荷トルクの確認